问题
问答题
如图,在四棱锥P—ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且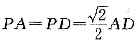
.
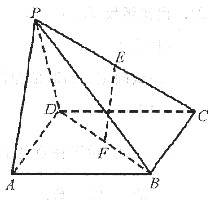
求证:平面PAB⊥平面PCD.
答案
参考答案:
[证明] 因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD。
又CD⊥AD,∴CD⊥平面PAD,∴CD⊥PA.
又[*],由勾股定理可得:△PAD是等腰直角三角形,且[*],即PA⊥PD,
又CD∩PD=D,∴PA⊥平面PCD,
又PA[*]平面PAB,∴平面PAB⊥平面PCD.
[*]
