问题
解答题
已知命题p：x1，x2是方程x2-mx-2=0的两个实根，不等式a2-5a-3≥|x1-x2|对任意实数m∈[-1，1]恒成立；命题q：不等式ax2+2x-1＞0有解，若命题“p∧q”为假命题，“p∨q”为真命题，求实数a的取值范围。
答案
解：∵x1，x2是方程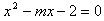
的两个实根，
∴
，
∴
，
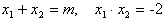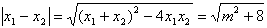∴当m∈[-1，1]时，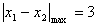
；
由不等式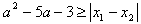
对任意实数m∈[-1，1]恒成立，
可得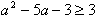
，解得
，
∴命题p为真命题时，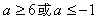
；
命题q：不等式
有解，
（1）当a＞0时，显然有解；
（2）当a=0时，2x-1＞0有解；
（3）当a＜0时，∵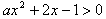
有解，
∴
，
∴
，
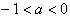∴命题q：不等式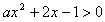
有解时a＞-1，
∵命题“p∧q”为假命题，“p∨q”为真命题，
∴命题p，q的真假性有两种情况：p真q假、p假q真，
当命题p真q假时，有
，得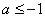
；
当p假q真时，有
，得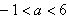
；
∴实数a的取值范围为a＜6。