问题
解答题
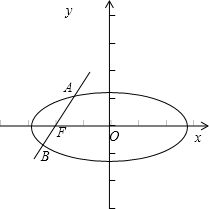
设椭圆C:
(1)求椭圆C的离心率; (2)如果|AB|=
|
答案
设A(x1,y1),B(x2,y2),由题意知y1>0,y2<0.
(1)直线l的方程为y=
(x+c),其中c=3
.a2-b2
联立
得 (3a2+b2)y2-2y=
(x+c)3
+x2 a2
=1y2 b2
b2cy-3b4=0.3
解得y1=
,y2=
b2(c+2a)3 3a2+b2
.
b2(c-2a)3 3a2+b2
因为
=2AF
,所以-y1=2y2.即-FB
=2
b2(c+2a)3 3a2+b2
,
b2(c-2a)3 3a2+b2
解得离心率e=
=c a
.(6分)2 3
(2)因为|AB|=
•|y2-y1|,∴1+ 1 k2
=15 4
•1+ 1 3
.4
ab23 3a2+b2
由
=c a
得b=2 3
a,所以5 3
a=5 4
,解得a=3,b=15 4
.5
故椭圆C的方程为
+x2 9
=1.(12分)y2 5