问题
问答题
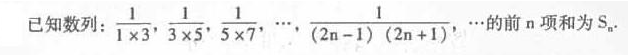
(1)计算s1,s2,s3的值;
(2)由(1)推测出Sn的计算公式,并用数学归纳法证明。
答案
参考答案:
(1)S1=1/(1×3)=1/3,S2=1/(1×3)+1/(3×5)=2/5,S3=2/5+1/(5×7)=3/7
(2)由(1)推测:Sn=n2n+1
证明:
①当n=1时成立。
②假设当n=k时成立,即Sk=k2k+1
则当n=k+1时,Sk+1=Sk+1
[2(k+1)-1][2(k+1)+1]=k2k+1+1(2k+1)(2k+3)=2k2+3k+1(2k+1)(2k+3)=k+12k+3=k+12(k+1)+1
即当n=k+1时成立
由①②得:Sn=n2n+1对任意n(n>1)成立。
