问题
解答题
设二次函数f(x)=x2+bx+c(b,c∈R),已知不论α、β为何实数恒有f(sinα)≥0和f(2+cosβ)≤0。
(1)求证: b+c=－1；
(2)求证c≥3；
(3)若函数f(sinα)的最大值为8，求b，c的值.
答案
(1)证明略(2)证明略(3) b=－4,c=3
(1)∵－1≤sinα≤1且f(sinα)≥0恒成立，∴f(1)≥0
∵1≤2+cosβ≤3,且f(2+cosβ)≤0恒成立
∴f(1)≤0.
从而知f(1)=0∴b+c+1=0
(2)由f(2+cosβ)≤0,知f(3)≤0,∴9+3b+c≤0 又因为b+c=－1,∴c≥3
(3)∵f(sinα)=sin2α+(－1－c)sinα+c=(sinα－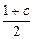
)2+c－(
)2,
当sinα=－1时，［f(sinα)］max=8,由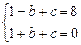
解得b=－4,c=3.