问题
问答题
设Y1,Y2,Y3独立,且都服从参数数为p的0-1分布.令
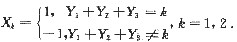
求:(1)(X1,X2)的联合分布律;
(2)p为何值时,E(X1X2)最小.
答案
参考答案:[详解] 令Y=Y1+Y2+Y3,则Y~B(3,P).
(1)P{X1=-1,X2=-1}=P{Y≠1,Y≠2}=P{Y=0}+P{Y=3}
=(1-p)3+p3,
P{X1=-1,X2=1}=P{Y≠1,Y=2}=P{Y=2}=3p2(1-p),
P{X1=1,X2=-1}=P{Y=1,Y≠2}=P{Y=1}=3p(1-p)2,
P{X1=1,X2=1}=P{Y=1,Y=2}=0.
所以,(X1,X2)的联合分布律为[*]
(2)E(X1X2)=(1-p)3+p3-3p2(1-p)-3p(1-p)2=1-6p+6p2,
所以,当[*]时,E(X1X2)取最小值[*].
解析:
[分析]: 如令Y=Y1+Y2+Y3,则由已知Y~B(3,p).求有关(X1,X2)的概率问题转化为与随机变量Y有关的概率.
[评注] 本题属于由已知分布的随机变量定义新的随机变量,讨论新随机变量的分布问题.
