问题
问答题
设函数ψ(y)具有连续导数，在围绕原点的任意分段光滑简单闭曲线L上，曲线积分
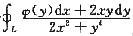的值恒为同一常数．
(Ⅰ)证明：对右半平面x＞0内的任意分段光滑简单闭曲线C，有
；
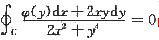(Ⅱ)求函数ψ(y)的表达式．
答案
参考答案：[详解] (Ⅰ)如图，将C分解为：C=l1+l2，另作一条曲线l3围绕原点且与C相接，则
[*]
[*]
(Ⅱ)利用(Ⅰ)的结果，知[*]
即有 -4x2y+2y5=ψ＇(y)(2x2+y4)-ψ(y)·4y3，
得 ψ＇(y)=-2y，yψ＇(y)-4ψ(y)=2y2，
解第一个微分方程，得ψ(y)=-y2+C，再代入第二个方程得C=0，故ψ(y)=-y2．
解析：
[分析]： 证明(Ⅰ)的关键是如何将封闭曲线C与围绕原点的任意分段光滑简单闭曲线相联系，这可利用曲线积分的可加性将C进行分解讨论；而(Ⅱ)中求ψ(y)的表达式，显然应用积分与路径无关即可．
[评注] 本题难度较大，关键是如何将待求解的问题转化为可利用已知条件的情形．