问题
填空题
等边三角形ABC与正方形ABDE有一公共边AB，二面角C—AB—D为直二面角，M，N分别是AC，BC的中点，则EM，AN所成角的余弦值为 ．
答案
设DE的中点为F，可证四边形MNFE为平行四边形，故ME//NF，∠ANF或其补角为异面直线AN，EM所成的角，在△ANF中，运用余弦定理求得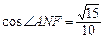
．
通过平移法求两条异面直线的夹角是本题的关键．
搜题请搜索小程序“爱下问搜题”
等边三角形ABC与正方形ABDE有一公共边AB，二面角C—AB—D为直二面角，M，N分别是AC，BC的中点，则EM，AN所成角的余弦值为 ．
设DE的中点为F，可证四边形MNFE为平行四边形，故ME//NF，∠ANF或其补角为异面直线AN，EM所成的角，在△ANF中，运用余弦定理求得．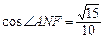
通过平移法求两条异面直线的夹角是本题的关键．