解：设，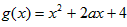

由于关于x的不等式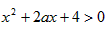对于一切x∈R恒成立，

所以函g（x）数的图象开口向上且与x轴没有交点，故，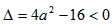

∴，

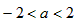函数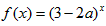是增函数，则有3-2a>1，即a<1，

由于p或q为真，p且q为假，可知p、q一真一假，

①若p真q假，则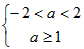

∴1≤a<2；

②若p假q真，则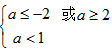

∴a≤-2；

综上可知，所求实数a的取值范围是｛a|1≤a<2或a≤-2｝。