设二次型f(x1,x2,x3)=
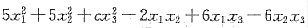 所对应的矩阵为A,且方程组Ax=0有非零解,
所对应的矩阵为A,且方程组Ax=0有非零解,
(Ⅰ)求c的值;
(Ⅱ)将二次型化为标准型,并写出正交变换矩阵.
参考答案:
解析: (Ⅰ)二次型对应的矩阵

因为方程组Ax=0有非零解,所以|A|=24c-72=0
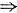 c=3.
c=3.
(Ⅱ)|λE-A|=
 =λ(λ-4)(λ-9)=0
=λ(λ-4)(λ-9)=0
则特征值为0,4,9.
将特征值分别代人(λE-A)x=0,可分别求得
λ=0对应的特征向量为:ξ1=
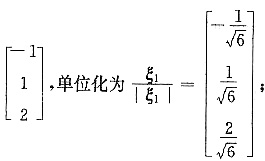
λ=4对应的特征向量为:ξ2=

λ=9对应的特征向量为:ξ3=
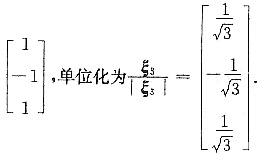
故二次型的标准型为
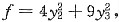 所作正交变换矩阵为
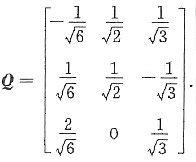
所作正交变换矩阵为

 6O2+X,则X的化学式: 。
6O2+X,则X的化学式: 。