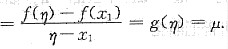问题
问答题
设函数f(x)在(a，b)内可导，x1与x2是(a，b)内的两点，g(x)由下式定义：
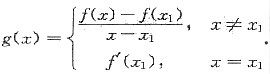
证明：对f’(x1)与g(x2)之间的任何值μ，在x1，与x2之间至少存在一点ξ，使f’(ξ)=μ.
答案
参考答案：[证] 不妨设x1＜x2，因为
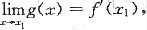可见g(x)在[x1，x2]上连续，由介值定理知，存在η∈[x1，x2]，g(η)=μ．
又根据拉格朗日中值定理，有
ξ∈(x1，η)
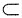(x1，x2)，使f’(ξ)
