问题
问答题
设二次型
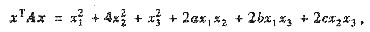
矩阵A满足AB=0,其中
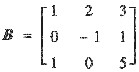 .
.
(Ⅰ) 用正交变换化二次型xTAx为标准形,并写出所用正交变换;
(Ⅱ) 求(A-3E)6.
答案
参考答案:(Ⅰ) 由[*]知,矩阵B的列向量是齐次方程组Ax=0的解向量.
记[*],则 Aα1=0=0α1,Aα2=0=0α2.
所以λ=0是矩阵A的特征值(至少是二重),α1,α2是λ=0的线性无关的特征向量.
根据∑λi=∑aii有0+0+λ3=1+4+1,故知矩阵A有特征值λ=6.因此,矩阵A的特征值是0,0,6.
设λ=6的特征向量为α3=(x1,x2,x3)T,那么由实对称矩阵不同特征值的特征向量相互正交,有
[*]解出α3=(1,2,-1)T.
对α1,α2正交化,令 β1=(1,0,1)T,则
[*]
再对β1,β2,α3单位化,得
[*]
那么经坐标变换X=Qy,即
[*]
二次型化为标准形[*].
(Ⅱ) 因为A~Λ,有A-3E~Λ-3E,进而(A-3E)6~(Λ-3E)6.又Λ-3E=[*],所以由Q-1AQ=Λ得Q-1(A-3E)6Q=(Λ-3E)6=36E.于是
(A-3E)6=Q(Λ-3E)6Q-1=Q(36E)Q-1=36E.
[*]
