问题
问答题
证明下列结论：
(Ⅰ) 设f(x，y)定义在全平面上，且
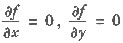，则f(x，y)恒为常数；
(Ⅱ) 设u(x，y)，v(x，y)定义在全平面上，且满足
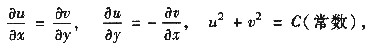
则u(x，y)，v(x，y)恒为常数．
答案
参考答案：(Ⅰ) 即证f(x，y)=f(0，0) ([*]x，y)．由于
[*]
因此 f(x，y)=f(0，0) ([*]x，y)．
(Ⅱ) 由所给条件我们将证明[*]
由[*]
将[*]代入上式[*]
此方程组的系数行列式
[*]
若C=0[*]u=0，v=0；若C≠0[*]u(x，y)为常数．
同理可证：v(x，y)为常数．
