设函数f(x)在[a,+∞)内二阶可导且f"(x)<0,又b>a,f(a)=A>0,f(b)=B>0,f’(b)<0,求证:
(Ⅰ)
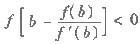 .
.
(Ⅱ) 方程f(x)=0在[a,+∞)内有且仅有一个实根.
参考答案:(Ⅰ) 方法1°f"(x)<0(x∈[a,+∞))[*]f(x)在[a,+∞)是凸函数[*]
f(x)<f(b)+f’(b)(x-b) (x∈[a,+∞),x≠b).
令[*]
方法2° 由泰勒公式可得
[*]
其中[*]
(Ⅱ) f(x)在[a,+∞)连续,f(b)>0,[*]在[*](a,+∞)有一个零点.
因f"(x)<0(x∈[a,+∞))[*]f’(x)在[0,+∞)↘.由f’(b)<0[*]f’(x)<0(x>b)[*]f(x)在[b,+∞)↘[*]f(x)在(b,+∞)只有唯一零点.
当x∈[a,b]时,由于f’(b)<0,f’(x)↘,只有以下两种情形:
1° f’(x)<0(x∈[a,b])[*]f(x)在[a,b]↘,如图(1)[*]
f(x)≥f(b)>0(x∈[a,b]);
2° [*]x0∈(a,b),如图(2),
[*]
f(x)>0(x∈[a,b]).
因此f(x)在[a,+∞)有唯一零点,即方程f(x)=0在[a,+∞)有且仅有一个实根.
[*]
