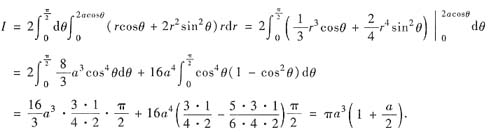问题
问答题
求二重积分
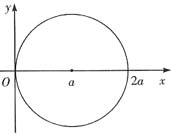
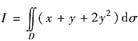 ,其中D是由圆周x2+y2=2ax所围成的区域,a>0为常数.
,其中D是由圆周x2+y2=2ax所围成的区域,a>0为常数.
答案
参考答案:[分析与求解] 圆域D:(x-α)2+y2≤α2关于x轴对称,于是
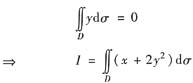
方法1° 作平移变换:u=x-α,υ=y,则D变成
D’:υ2+υ2≤α2,
D’关于υ轴对称,它的面积为πα2,于是
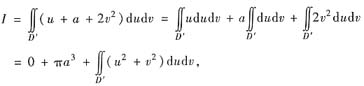
这里由变量的轮换对称性知
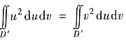
再作极坐标变换,有
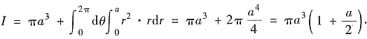
方法2° 记
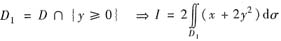
用先y后x的积分顺序,
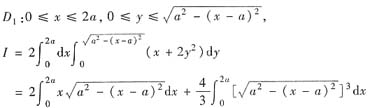 对第一个积分,令t=x-α;对第二个积分,令x-α=αsint
对第一个积分,令t=x-α;对第二个积分,令x-α=αsint
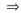
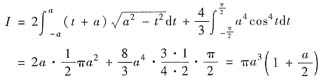
方法3°
 直接作极坐标变换,则圆周x2+y2=2αx的极坐标方程是r=2αcosθ,于是
直接作极坐标变换,则圆周x2+y2=2αx的极坐标方程是r=2αcosθ,于是
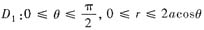 ,且
,且