问题
问答题
已知α1=(1，2，0)，α2=(1，a+2，-3a)，α3=(-1，b+2，a+2b)，及β=(1，3，-3)，求：
(Ⅰ)a，b为何值时，β不能表示成α1，α2，α3的线性组合；
(Ⅱ)a，b为何值时，β有α1，α2，α3的唯一线性表示，并写出该表达式．
答案
参考答案：
解析： (Ⅰ)设β=x1α1+x2α2+x3α3，于是
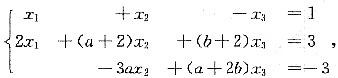
增广矩阵A=
当a=0，且b为任意常数时，有
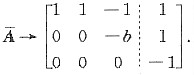
可知r(A)≠r(
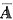)，故此时方程组无解，即β不能表示成α1，α2，α3的线性组合．
(Ⅱ)当a≠0且a≠b时，r(A)=r(
)=3，此时方程组有唯一解
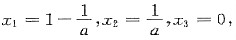
则β有α1，α2，α3的唯一线性表示，且
