问题
解答题
(本小题满分12分)
已知p:方程x2+mx+1=0有两个不相等的负实根;q:不等式4x2+4(m-2)x+1>0的解集为R,若p或q为真命题,p且q为假命题,求m的取值范围.
答案
解:
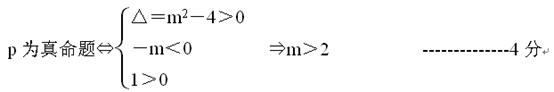
q为真命题⇔△=[4(m-2)]2-4×4×1<0⇒1<m<3. ------------8分
∵p或q为真,p且q为假,∴p与q一真一假.
若p真q假,则m>2,且m≤1或m≥3,所以m≥3.
若p假q真,则m≤2,且1<m<3,所以1<m≤2.
综上所述,m的取值范围为{m|1<m≤2,或m≥3}. -----------12分
