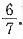问题
问答题
求由方程2x2+2y2+z2+8xz-z+6=0所确定的隐函数z=z(x，y)的极值．
答案
参考答案：
解析： 在方程2x2+2y2+z2+8xz-z+6=0两边取微分可得
4xdx+4ydy+2zdz+8(xdz+zdx)-dz=0，
整理可得
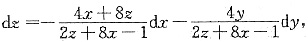于是
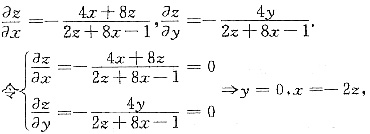
代入方程2x2+2y2+z2+8xz-z+6=0可得
7z2+z-6=0
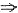(7z-6)(z+1)=0
z1=-1，z2=
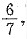
于是驻点为(2，0)和(
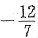，0)．
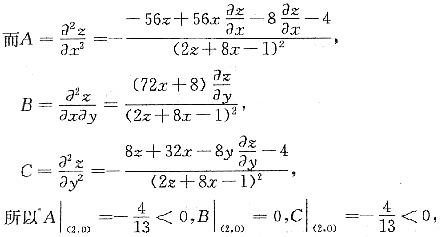
且(B2-AC)｜(2，0)＜0，
所以函数z=z(x，y)在点(2，0)处取得极大值z=-1．
又
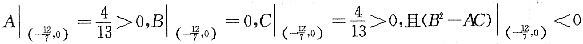
所以函数z=z(x，y)在点(
，0)处取得极小值z=
