问题
问答题
设A是二阶矩阵，α为非零向量，但不是A的特征向量，且满足A2α+Aα-2α=0．
证明：
(Ⅰ)α，Aα线性无关；
(Ⅱ)A可对角化．
答案
参考答案：[证] (Ⅰ)设存在走k1，k2，使得k1α-k2Aα=0．
若
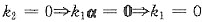(因为α≠0)，
若
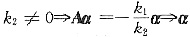是A的特征向量，矛盾．
综上，可得k1=k2=0，所以α，Aα线性无关.
(Ⅱ)由A2α+Aα-2α=0
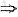(A2+A-2E)α=0，
因为α是非零向量，所以齐次方程组(A2+A-2E)x=0有非零解，于是有
｜A2+A-2E｜=0
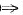｜A+2E｜｜A-E｜=0，即｜A+2E｜=0或｜A-E｜=0．
若｜A+2E｜≠0，则由(A+2E)(A-E)α=0
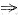(A-E)α=0
Aα=α，即α是A的特征向量，矛盾，所以｜A+2E｜=0；同理可证｜A-E｜=0．
所以A有两个不同的特征值λ1=-2，λ2=1，故二阶矩阵A有两个线性无关的特征向量，即A可对角化．