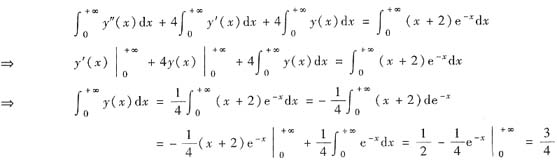问题
问答题
已知
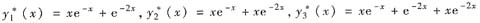是某二阶线性
常系数微分方程y’’+Py’+qy=f(x)的三个特解．
(Ⅰ) 求这个方程和它的通解；
(Ⅱ) 设y=y(x)是该方程满足y(0)=0，y’(0)=0的特解，求
答案
参考答案：[分析与求解] (Ⅰ)由线性方程解的叠加原理
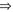
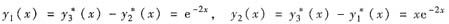
均是相应的齐次方程的解，它们是线性无关的．于是相应的特征方程为
(λ+2)2=0，即λ2+4λ+4=0，
原方程为 y’’+4y’+4y=f(x)．(*)
又y*(x)=xe-x是它的特解，求导得
Y’’(x)=e-x(1-x)，y*’’(x)=e-x(x-2)．
代入方程(*)得
e-x(x-2)+4e-x(1-x)+4xe-x=f(x)
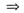f(x)=(x+2)e-x
所求方程为y’’+4y’+4y=(x+2)e-x其通解为
y=C1e-2x+C2xe-2x+xe-x，其中C1，C2为
常数．
(Ⅱ)
C1，C2，方程的任意解y(x)均有
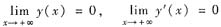
不必由初值来定C1，C2，直接将方程两边积分得
