问题
问答题
设正项级数
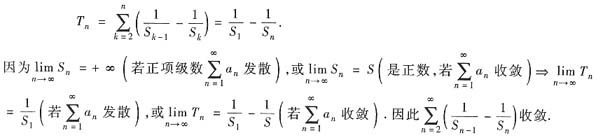是它的部分和．
(Ⅰ) 求证：
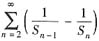收敛；
(Ⅱ) 判断级数
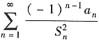是条件收敛还是绝对收敛，并给予证明
答案
参考答案：[分析与证明] (Ⅰ)级数
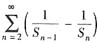的部分和Tn易求出
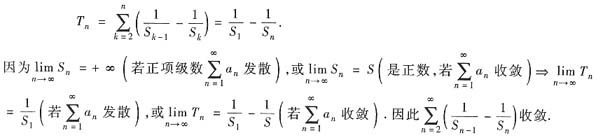
(Ⅱ)考察级数
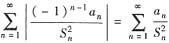由Sn与an的关系：
Sn=α1+α2+…+αn-1+αn，αn=Sn-Sn-1，
将一般项
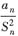改写成只与Sn有关，即
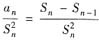
因正项级数的部分和数列Sn单调上升，上式可放大成
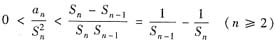
由题(Ⅰ)
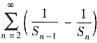收敛，再由比较原理知，
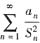收敛．因此，原级数绝对收敛．