问题
问答题
设
 ,当r≠0时有连续的二阶偏导数且满足
,当r≠0时有连续的二阶偏导数且满足

求函数u(x,y).
答案
参考答案:[分析与求解] 由复合函数求导法,建立u对x,y的偏导数与u对r的导数的关系,把题设方程
(*)转化为u(r)的常微分方程,然后求出u(r).
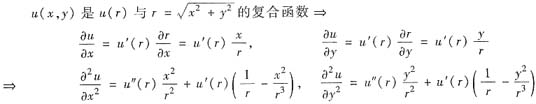
将它们相加得
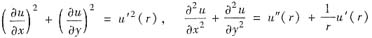
于是题设方程(*)变成
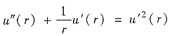
令P=u’(r),降阶得
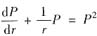 .这是伯努利方程,改写成
.这是伯努利方程,改写成
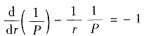
两边乘
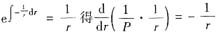 积分得
积分得
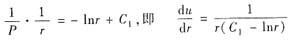
再积分得
 其中C1,C2为任意常数.
其中C1,C2为任意常数.
