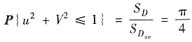问题
问答题
设二维随机变量(X,Y)的密度函数为

(Ⅰ) 问X,Y是否独立
(Ⅱ) 分别求U=X2和V=Y2的密度函数fU(u)和fV(v),并指出(U,V)所服从的分布;
(Ⅲ) 求PU2+V2≤1.
答案
参考答案:[解] (Ⅰ)
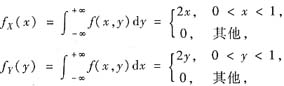
由于f(x,y)=fX(x)·fY(y),(x,y)∈R2,故X,Y相互独立.
(Ⅱ)
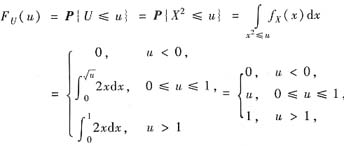
所以
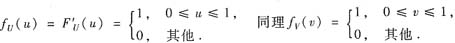
由于X,Y相互独立,所以U=X2和V=Y2也相互独立,从而(U,V)的密度函数为
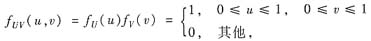
由此表明,(U,V)服从区域Duυ={(u,υ)|0≤u≤1,0≤υ≤1}上的均匀分布.
(Ⅲ)由(Ⅱ)可知(记D={(u,υ)|u2+υ2≤1,u≥0,υ≥0})