问题
解答题
在ABC中,内角A,B,C的对边分别为a,b,c,已知
(Ⅰ)求
(Ⅱ)若cosB=
|
答案
(Ⅰ)由正弦定理设
=a sinA
=b sinB
=kc sinC
则
=2c-a b
=2ksinC-ksinA ksinB
=2sinC-sinA sinB cosA-2cosC cosB
整理求得sin(A+B)=2sin(B+C)
又A+B+C=π
∴sinC=2sinA,即
=2sinC sinA
(Ⅱ)由余弦定理可知cosB=
=a2+c2-b2 2ac
①1 4
由(Ⅰ)可知
=sinC sinA
=2②c a
①②联立求得c=2,a=1
sinB=
=1- 1 16 15 4
∴S=
acsinB=1 2 15 4

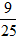 )g
)g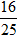 )g
)g