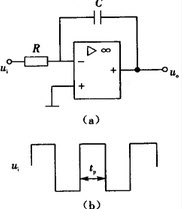
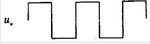
问题
解答题
| 已知圆x2+y2=25,△ABC内接于此圆,A点的坐标(3,4),O为坐标原点. (1)若△ABC的重心是G(
(2)若直线AB与直线AC的倾斜角互补,求证:直线BC的斜率为定值. |
答案
设B(x1,y1),C(x2,y2),
由题意可得:
=x1+x2+3 3 5 3
=2y1+y2+4 3
即
,
=1x1+x2 2
=1y1+y2 2
又
,
+x 21
=25y 21
+x 22
=25y 22
相减得:(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0,
∴
=-1y1-y2 x1-x2
∴直线BC的方程为y-1=-(x-1),即x+y-2=0
(2)设AB:y=k(x-3)+4,代入圆的方程整理得:
(1+k2)x2+(8k-6k2)x+9k2-24k-9=0
∵3,x1是上述方程的两根,
∴x1=
,y1=3k2-8k-3 1+k2 -4k2-6k+4 1+k2
同理可得:x2=
,y2=3k2+8k-3 1+k2 -4k2+6k+4 1+k2
∴kBC=
=y1-y2 x1-x2 3 4