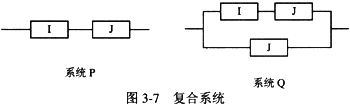
一个复杂的系统可由若干个简单的系统串联或并联构成。已知两个简单系统I和J的失效率分别为λI=25×10-5/h(小时)和λJ=5×104/h(小时),则由I和J经如图3-7所示的串联和并联构成的复合系统P和Q的失效率分别为λP= (15) /h和λQ= (16) /h。平均无故障时间分别为MTBFP= (17) h和MTBFQ= (18) h。系统P开始运行后2万小时内能正常运行的概率RP= (19) 。
A.e-5
B.e-10
C.e-15
D.e-20
参考答案:C
解析:
[分析]:
在本题中,系统P是一个简单的串联系统,其失效率为:
λP=λI+λJ=25×10-5+5×10-4=75×10-5
系统Q把两个I部件串联后再与部件J进行并联。两个I部件串联后的失效率为:
λI+λI=25×10-5+25×10-5=50×10-5=5×10-4
也就是说,两个I部件串联后的失效率与一个J部件的失效率是相等的。因此,根据并联系统的公式,可以得到系统Q的总失效率为:
λQ=5×10-4/(1+1/2)=10-3/3≈33×10-5
平均无故障时间与失效率的关系为MTBF=1/λ,因此
MTBFP=1/(75×10-5)≈1333h;MTBFQ=1/(33×10-5)≈3000h
系统的可靠性只与失效率的关系为R=e-λt,因此,当t为2万小时(2×104)时,可得
λ×t=75×10-5×2×104=15
