问题
问答题
设三元二次型xTAx经正交变换化为标准形
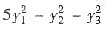 ,若Aα=5α,其中α=(1,1,1)T,求此二次型的表达式.
,若Aα=5α,其中α=(1,1,1)T,求此二次型的表达式.
答案
参考答案:[解] 二次型经正交变换化为标准形[*],知矩阵A的特征值是5,-1,-1.设λ=-1的特征向量是β=(x1,x2,x3)T,由于A是实对称矩阵,故α与β正交,则有
x1+x2+x3=0.
解出β1=(-1,1,0)T,β2=(-1,0,1)T.
那么令
[*]
于是
[*]
所以[*]
解析:
[*]

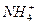 +Cl-,NH4Cl属于盐
+Cl-,NH4Cl属于盐