问题
问答题
已知
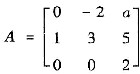有三个线性无关的特征向量，则a=______．
答案
参考答案：先求矩阵A的特征值，由
[*]
知矩阵A的特征值是λ1=1，λ2=λ3=2．
因为矩阵A有三个线性无关的特征向量，λ=2是二重特征值，故λ=2必有两个线性无关的特征向量，那么秩r(2E-A)=1．
[*]
所以a=-10．
搜题请搜索小程序“爱下问搜题”
已知
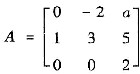有三个线性无关的特征向量，则a=______．
参考答案：先求矩阵A的特征值，由
[*]
知矩阵A的特征值是λ1=1，λ2=λ3=2．
因为矩阵A有三个线性无关的特征向量，λ=2是二重特征值，故λ=2必有两个线性无关的特征向量，那么秩r(2E-A)=1．
[*]
所以a=-10．