| 圆x2+y2=8内有一点P0(-1,2),AB为过点P0且倾斜角为α的弦; (1)当a=
(2)当弦AB被点P0平分时,求直线AB的方程. |
(1)直线AB的斜率k=tan
=-1,3π 4
∴直线AB的方程为y-2=-(x+1),即x+y-1=0
∵圆心O(0,0)到直线AB的距离d=
=|-1| 2 2 2
∴弦长|AB|=2
=2r2-d2
=8- 1 2
.30
(2)∵P0为AB的中点,OA=OB=r,
∴OP0⊥AB
又kOP0=
=-2,∴kAB=2-0 -1-0 1 2
∴直线AB的方程为y-2=
(x+1),即x-2y+5=01 2

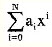 中有许多系数为零时,可用一个单链表来存储,每个节点存储一个非零项的指数和对应系数。
中有许多系数为零时,可用一个单链表来存储,每个节点存储一个非零项的指数和对应系数。