已知矩阵A和B相似,其中
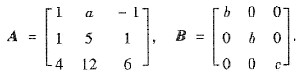
求a,b,c的值.
参考答案:[解] 由于矩阵A与对角矩阵B相似,知矩阵A的特征值是b,b,c.且λ=b有两个线性无关的特征向量,故秩r(bE-A)=1.
矩阵A的特征多项式
[*]
若b=2,则λ2-10λ+13-a必含有λ-2的因式.于是
22-20+13-a=0[*]a=-3.
再由 1+5+6=b+b+c [*]c=8.此时,
[*]
故a=-3,b=2,c=8合于所求.
若c=2,则由1+5+6=b+b+c知b=5.
于是λ2-10λ+13-a=(λ-5)2,解出a=-12.因为
[*]
说明λ=5只有1个线性无关的特征向量,因而矩阵A不能相似对角化.故这组数应舍去.
解析:
[*]
