问题
单项选择题
设α1,α2,α3,α4是4元非齐次线性方程组Ax=b的4个解向量,且α1+α2=(2,4,6,8)T,α2+α3+α4=(3,5,7,9)T,α1+2α2-α3=(2,0,0,2)T,若秩r(A)=2,则方程组Ax=b的通解是
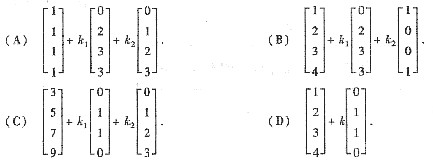
答案
参考答案:A
解析:
[分析]: 因为方程组Ax=b有解,且秩r(A)=2,那么n-r(A)=4-2=2,故通解形式为α+k1η1+k2η2.显然(D)不符合解的结构,应排除.(C)中(3,5,7,9)T不是Ax=b的解也应排除.下面应当用解的性质分析出特解α及导出组的基础解系.
由于A(α1+α2)=2b,有[*],因此(1,2,3,4)T是方程组Ax=b的一个解.又
(α2+α3+α4)-(α1+α2)=α3+(α4-α1)=(1,1,1,1)T也是方程组Ax=b的解.而
(α1+α2)-(α1+2α2-α3)=α3-α2=(0,4,6,6)T,
3(α1+α2)-2(α2+α3+α4)=2(α1-α3)+(α1-α4)+(α2-α4)=(0,2,4,6)T是导出组Ax=0的解.
故应选(A).
