问题
问答题
已知A是3阶实对称矩阵，若有正交矩阵P使得
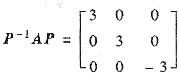．且α1=
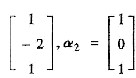是矩阵A属于特征值A=3的特征向量，则P=______．
答案
参考答案：因为实对称矩阵属于不同特征值的特征向量互相正交．设属于λ=-3的特征向量α3=x1，x2，x3)T，则
[*]
由于现在属于λ=3的特征向量α1，α2不正交，故应schmidt正交化处理．
令[*]
把β1，β2，β3单位化，得
[*]
那么P=[*]为所求．
解析：
[*]