问题
问答题
已知矩阵
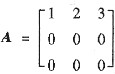 和
和
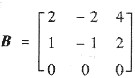 ,试求可逆矩阵P,使P-1AP=B.
,试求可逆矩阵P,使P-1AP=B.
答案
参考答案:[解] 由[*],得到矩阵A的特征值:λ1=λ2=0,λ3=1.
对应于λ1=λ2=0,解齐次线性方程组(0E-A)x=0,得基础解系:
α1=(-2,1,0)T,α2=(-3,0,1)T.
对应于λ3=1,解齐次线性方程组(E-A)x=0,得基础解系:α3=(1,0,0)T.
令
[*]
由
[*],得到矩阵B的特征值:λ1=λ2=0,λ3=1.
对应于λ1=λ2=0,解齐次线性方程组(0E-B)x=0,得基础解系:
β1=(1,1,0)T,β2=(-2,0,1)T.
对应于λ3=1,解齐次线性方程组(E-B)x=0,得基础解系:β3=(2,1,0)T.
令
[*]
由[*]
记[*]
P即为所求可逆矩阵.
解析:
[分析]: 因为A和B均与对角矩阵[*]相似,可有
[*]
从而[*],可知P-1AP=B,其中[*]
