问题
问答题
已知
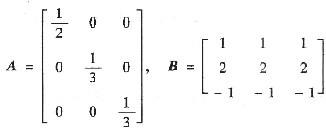，矩阵X满足XA-AB=AXA-ABA，则X3=______．
答案
参考答案：化简矩阵方程 XA-AXA=AB-ABA，得(E-A)XA=AB(E-A)．
因为A，E-A均可逆，故
X=(E-A)-1AB(E-A)A-1=(A-1-E)-1B(A-1-E)．
那么 X3=(A-1-E)-1B3(A-1-E)．
因为秩r(B)=1，有B2=2B．从而得B3=22B=4B．于是
[*]
解析：[*]