问题
问答题
设
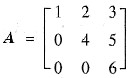 ,则|2A-1+E|=______.
,则|2A-1+E|=______.
答案
参考答案:[分析一] 由于|2A-1+E|=|A-1(2E+A)|=|A-1||2E+A|,因为|A|=24,故[*].又
[*]
从而 |2A-1+E|=6.
[分析二] 由A是上三角矩阵易知矩阵A的特征值是1,4,6,那么A-1的特征值是[*];2A-1的特征值是[*];2A-1+E的特征值是[*].从而
[*]
解析:[*]
设
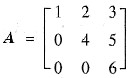 ,则|2A-1+E|=______.
,则|2A-1+E|=______.
参考答案:[分析一] 由于|2A-1+E|=|A-1(2E+A)|=|A-1||2E+A|,因为|A|=24,故[*].又
[*]
从而 |2A-1+E|=6.
[分析二] 由A是上三角矩阵易知矩阵A的特征值是1,4,6,那么A-1的特征值是[*];2A-1的特征值是[*];2A-1+E的特征值是[*].从而
[*]
解析:[*]