问题
问答题
已知A=-E+αβT,其中
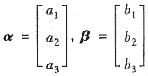 ,且αTβ=3,证明A可逆并求A-1.
,且αTβ=3,证明A可逆并求A-1.
答案
参考答案:[证明] (用特征值、用定义) 记B=αβT,则A=-E+B.而
[*]
由于r(B)=1,αTβ=a1b1+a2b2+a3b3=3,故
|λE-B|=λ3-(a1b1+a2b2+a3b3)λ2=λ3-3λ2.
所以矩阵B的特征值是3,0,0.
那么,矩阵A的特征值是2,-1,-1,故A可逆.
因为αTβ=βTα=3,有 β2=(αβT)(αβT)=α(βTα)βT=3B.
于是 (A+E)2=3(A+E).
即 A2-A=2E,亦即[*]
所以[*]
解析:[*]
