问题
问答题
已知矩阵
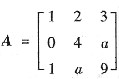中a＜0，且齐次方程组Ax=0有非零解，A*是A的伴随矩阵，则齐次方程组A*x=0的通解是______．
答案
参考答案：因为齐次方程组Ax=0有非零解，故
[*]
于是a=6或a=-4．又因a＜0，从而a=-4．
因为秩r(A)=2，所以r(A*)=1．于是齐次方程组A*x=0有n-r(A*)=3-1=2个线性无关的解．
又因A*A=|A|E=0，所以矩阵A的列向量是A*x=0的解．故A*x=0的通解是
k1(1，0，1)T+k2(1，2，-2)T，其中k1，k2为任意常数．
解析：
[*]