问题
选择题
由命题“存在x∈R,使e|x-1|-m≤0”是假命题,得m的取值范围是(-∞,a),则实数a的取值是( )
A.(-∞,1)
B.(-∞,2)
C.1
D.2
答案
答案:C
题目分析:命题“存在x∈R,使e|x-1|-m≤0”是假命题,则命题 是真命题,即不等式
是真命题,即不等式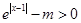 恒成立,
恒成立,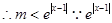 最小值为1
最小值为1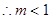
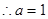
点评:特称命题的否定是全称命题,不等式恒成立求参数范围常采用分离参数,转化为求函数最值问题
由命题“存在x∈R,使e|x-1|-m≤0”是假命题,得m的取值范围是(-∞,a),则实数a的取值是( )
A.(-∞,1)
B.(-∞,2)
C.1
D.2
答案:C
题目分析:命题“存在x∈R,使e|x-1|-m≤0”是假命题,则命题 是真命题,即不等式
是真命题,即不等式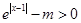 恒成立,
恒成立,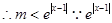 最小值为1
最小值为1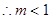
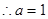
点评:特称命题的否定是全称命题,不等式恒成立求参数范围常采用分离参数,转化为求函数最值问题