问题
选择题
已知命题p：“∀x∈R，∃m∈R，使4x＋2x·m＋1＝0”．若命题p为真命题，则实数m的取值范围是
A．(－∞，－2]
B．[2,+∞)
C．(－∞，－2)
D．(2,+∞)
答案
答案：A
因为p为真命题，即方程4x＋2x·m＋1＝0有实数解，所以－m＝2x＋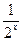
≥2，所以m≤－2，
故m的取值范围是(－∞，－2]．
搜题请搜索小程序“爱下问搜题”
已知命题p：“∀x∈R，∃m∈R，使4x＋2x·m＋1＝0”．若命题p为真命题，则实数m的取值范围是
A．(－∞，－2]
B．[2,+∞)
C．(－∞，－2)
D．(2,+∞)
答案：A
因为p为真命题，即方程4x＋2x·m＋1＝0有实数解，所以－m＝2x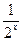＋≥2，所以m≤－2，
故m的取值范围是(－∞，－2]．