问题
问答题
已知函数f(u)具有二阶导数,且f’(0)=1,函数y=y(x)由方程y-xey-1=1所确定.设z=f(lny-sinx),求
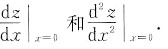
答案
参考答案:[*]
[*]
在y-xey-1=1中,令x=0,得y=1.由y-xey-1=1,两边对x求导,得
y’-ey-1-xey-1y’=0.
再对x求导,得
y"-ey-1y’-ey-1y’-xey-1y’2-xey-1y"=0.
将x=0,y=1代入上面两式得y’(0)=1,y"(0)=2,故
[*]
解析:[考点提示] 隐函数的求导.
