问题
证明题
设数列{an}、{bn}、{cn}满足:bn=an-an+2,cn=an+2an+1+3an+2(n=1,2,3,…),证明:{an}为等差数列的充分必要条件是{cn}为等差数列且bn≤bn+1(n=1,2,3,…)。
答案
解:必要性:设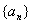 是公差为d1的等差数列,则
是公差为d1的等差数列,则
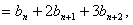
所以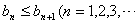 )成立
)成立
又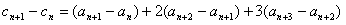
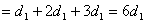 (常数)(n=1,2,3,…),
(常数)(n=1,2,3,…),
所以数列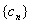 为等差数列;
为等差数列;
充分性:设数列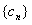 是公差d2的等差数列,且
是公差d2的等差数列,且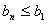 (n=1,2,3,…)
(n=1,2,3,…)
∵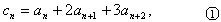
∴
①-②得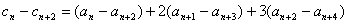
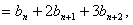
∵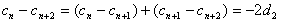
∴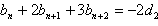 ③
③
从而有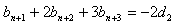 ④
④
④-③得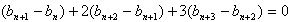 ⑤
⑤
∵
由⑤得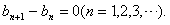
由此不妨设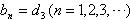
则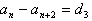 (常数)
(常数)
由此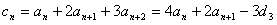
从而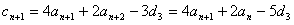
两式相减得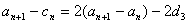
因此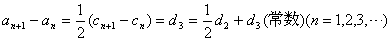
所以数列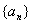 是等差数列。
是等差数列。
