问题
填空题
已知曲线y=f(x)过点(0，-
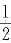)，且其上任一点(x，y)处的切线斜率为xln(1+x2)，则f(x)=______．
答案
参考答案：[*](1+x2)[ln(1+x2)-1]
解析：[考点提示] 导数的几何意义．
[解题分析] 由导数的几何意义建立一阶微分方程，求解方程即得曲线方程，
[详解] 由已知，得y’=xln(1+x2)，于是
[*]
代入条件：y(0)=[*]，得C=-[*]
所以f(x)=[*](1+x2)[ln(1+x2)-1]．