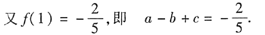问题
问答题
已知函数f(x)=ax3-bx2+cx在区间(-∞，+∞)内是奇函数，且当 x=1时f(x)有极小值
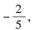，求a，b，c．
答案
参考答案：
解析：本题考查的知识点是奇函数的概念、极值的概念及极值的必要条件．
[分析]： 如果函数是一个m次多项式，且是奇(或偶)函数，则一定有偶次幂(或奇次幂)项的系数为0．再利用极值的必要条件及极值即可求出a，b，c
解 因为f(-x)=-f(x)，即
-ax3-bx2-cx=-ax3+bx2-cx
得 2bx2=0 对a∈R都成立，必有b=0．
由极值的必要条件：f’(1)=0，得3a-2b+c=0，解得
