某城市为稳定冬季蔬菜的供应,计划在郊区兴建和扩建大型温室。根据对历史数据的调查,温室的建造面积和建造成本的关系见表4-1。
表4-1 温室的建造面积和建造成本的关系
| 建造面积x/万m2 | 建造成本y/万元 | 建造面积x/万m2 | 建造成本y/万元 | 建造面积x/万m2 | 建造成本y/万元 |
| 4 | 14.8 | 5 | 16.7 | 5 | 16.9 |
| 7 | 25.1 | 8 | 29.1 | 4 | 15.1 |
| 2 | 12.4 | 6 | 21.8 | 9 | 33.2 |
| 3 | 13.5 |
[问题]
1.求建造面积与建造成本的回归直线方程(回归模型:y=a+bx)。
2.在5%的显著性水平下对建造面积和建造成本进行相关性检验。
3.给定显著水平α=5%,对b进行相关性检验和显著性检验(t检验法),说明显著性水平为5%所代表的意义。
4.假定根据测算,计划兴建的温室面积约为11万m2,利用回归方程预测建设成本,给出置信度为95%的预测区间,并对预测区间和置信度作出经济解释。
已知 ∑xiyi=1191
t(0.05,10)=1.8125,t(0.05,8)=1.8595
t(0.025,10)=2.2281,t(0.025,8)=2.3060
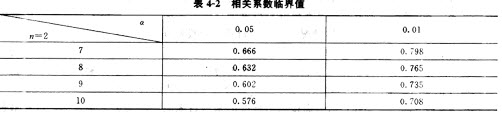
相关系数临界值表的部分见表4-2。
参考答案:
设建造成本为因变量y,以建筑面积为自变量x,建立一元回归模型:y=a+bx。
其中,a为回归常数,b为回归系数。
列表计算需要的数据,见表4-6。
[*]
[*]
采用最小二乘法,得
[*]
回归方程:y=3.2244+2.1388x
2.相关检验:
[*]
由相关系数临界值表查得α=0.05,自由度n-2=10-2=8时,R0.05=0.632。因R= 0.9743>0.632=R0.05,所以在5%的显著性水平下,检验通过,说明建筑面积与建造成本的线性关系合理。
3.显著性检验(t检验):
[*]
已知t(0.025,8)=2.306,tb=12.2415>2.306=t(0.025,8),所以在5%的显著性水平下,t检验通过,说明建筑面积与建造成本的线性关系明显。
4.建设成本的点预测:
当建筑面积为11万m2时,建设成本为:
y’0=a+bxi=(3.2244+3.1388×11)万元=37.75万元
区间预测:
[*]
[*]
所以在置信度为95%时,建造成本的置信区间为:
y’0±ta/2S0=37.75±2.306×2.3077=37.75±5.32
即(32.43,43.07)。
预测区间可以反映出预测的偏离范围;置信度表示预测结果的可靠程度。
