Dye (染料) can bring a little color to life. Most clothing is colored with dyes. Modern, manufactured dyes can be costly. Natural dyes from plant and animal products have been used since ancient times. So this week, we describe a natural way to dye wool.
There are several methods to put dye onto material. The vat method, for example, can be used to dye wool with onionskins. For this example, use one hundred grams of natural wool. The wool must be clean. Leave it overnight in water and liquid soap. Then wash it with clean water that is a little warm. Gently squeeze out the extra water.
A solution called a mordant (媒染) is used in the dying process. A mordant helps fix the dye to the material. Traditionally, mordants were found in nature. Wool ash is one example. But chemical mordants such as alum are popular today. Alum is sold in many stores. It is often mixed with cream of tartar, a fine powder commonly used in cooking.
Mix eight grams of alum with seven grams of cream of tartar in a small amount of hot water. Add the solution to a metal pan of cool water. Next, add the wool and place the mixture over heat. Slowly bring the liquid to eighty-two degrees Celsius. Heat the mixture for forty-five minutes. After it cools, remove the wool and wash it.
To prepare the dye solution, cover thirty grams of onionskins with water. Use only the dry, brown outer skins. Boil the liquid until the onionskins lose their color, about forty-five minutes. Remove the skins after the dye cools.
Now it is time to dye the wool. Place the wool into the dye and heat the mixture. Bring it to a boil, then immediately reduce the heat to eighty-two degrees. Now heat the dye for about forty-five minutes or until the wool is the desired color. Keep in mind that wet wool looks darker than it is.
Once the dye cools, remove the wool and wash it. Now the wool is orange or yellow. Or at least it should be.
57. According to the passage, mordants are ________.
A. dyes used in the dying process
B. materials which will be put dye to
C. wood ashes used in the dying process
D. not dyes but play an important role in the dying process
58. Which of the following statements about “natural dyes” is true?
A. They might be cheaper than chemical dyes.
B. They are more expensive than chemical dyes.
C. They have been used for only recent years.
D. They are all made from animal products.
59. As for the vat method, which of the following statements is NOT necessarily needed?
A. Ash. B. Water. C. Mordant. D. Temperature.
60. Choose the proper order of dying wool:
a. boil the liquid with onionskins.
b. add mordants to a metal pan of cool water.
c. wash the wool with clean water.
d. put the wool into the liquid and heat it
e. heat the mixture and then wash it.
A. c, b, e, a, d B. e, b, c, d, a C. b, e, a, d, c D. a, b, e, c, d
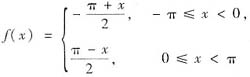 展开成以2π为周期的傅里叶级数.
展开成以2π为周期的傅里叶级数.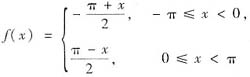 展开成以2π为周期的傅里叶级数.
展开成以2π为周期的傅里叶级数.