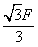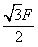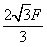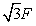问题
填空题
实数x,y满足tanx=x,tany=y,且|x|≠|y|,则
|
答案
tanx=
=xsinx cosx
∴sinx=xcosx
同理,siny=ycosy
所以原式=
-sinxcosy+cosxsiny x+y sinxcosy-cosxsiny x-y
=
-xcosxcosy-ycosxcosy x-y xcosxcosy+ycosxcosy x+y
=
-cosxcosy(x+y) x+y cosxcosy(x-y) x-y
=cosxcosy-cosxcosy
=0
故答案为:0

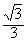 F,方向未知,则F1的大小可能是[ ]
F,方向未知,则F1的大小可能是[ ]