问题
问答题
将函数
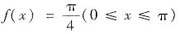展开成正弦级数，并求级数
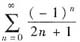的和．
答案
参考答案：将函数[*]延拓为[-π，π]上的奇函数F(x)，则傅里叶系数
an=0，
[*]
所以
[*]
由于傅里叶级数的和函数满足：S(0)=0，S(π)=0，从而S(0)≠f(0)，S(π)≠f(π)，所以函数[*]展开成正弦级数为
[*]
因此
[*]
搜题请搜索小程序“爱下问搜题”
将函数
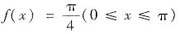展开成正弦级数，并求级数
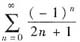的和．
参考答案：将函数[*]延拓为[-π，π]上的奇函数F(x)，则傅里叶系数
an=0，
[*]
所以
[*]
由于傅里叶级数的和函数满足：S(0)=0，S(π)=0，从而S(0)≠f(0)，S(π)≠f(π)，所以函数[*]展开成正弦级数为
[*]
因此
[*]