问题
问答题
设f(x)在|x|≤1有一阶连续导数且
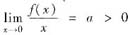 ,证明级数
,证明级数
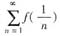 发散而级数
发散而级数
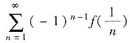 收敛.
收敛.
答案
参考答案:(1)由[*]得[*],根据极限的保号性质可得:存在N当n>N时[*],即级数[*]是正项级数,并由比较判别法的极限形式知[*]发散,而级数是否敛散与其前有限项无关,故[*]发散.
(2)由上面分析知当n充分大以后级数[*]是交错级数.
由于[*],所以f(0)=0,f’(0)=a>0,因为f’(x)在x=0处连续,所以存在x=0的某个邻域U,使得[*],都有f’(x)>0,即f(x)在U内单调增加,故当n充分大时,[*]随n变大而减小且[*].根据莱布尼兹判别法知[*]收敛.
