某施工单位编制的某工程网络图,如图1所示,网络进度计划原始方案各工作的持续时问和估计费用,见表2。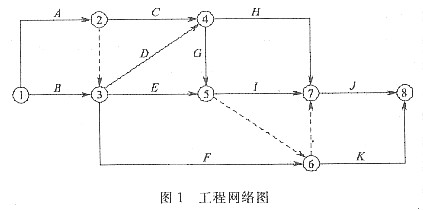
| 表2 各工作持续时间和估计费用表 | |||||
| 工作 | 持续时间/d | 费用/万元 | 工作 | 持续时间/d | 费用/万元 |
| A | 12 | 18 | G | 8 | 16 |
| B | 26 | 40 | H | 28 | 37 |
| C | 24 | 25 | I | 4 | 10 |
| D | 6 | 15 | J | 32 | 64 |
| E | 12 | 40 | K | 16 | 16 |
| F | 40 | 120 | |||
问题:
该网络进度计划各工作的可压缩时间及压缩单位时间增加的费用,见表3。确定该网络进度计划的最低综合费用和相应的关键路线,并计算调整优化后的总工期(要求写出调整优化过程)。
| 表3 各工作可压缩时间和增加费用表 | |||||
| 工作 | 可压缩时间 /d | 压缩单位时间增加 的费用/(万元/d) | 工作 | 可压缩时间 /d | 压缩单位时间增加 的费用/(万元/d) |
| A | 2 | 2 | G | 1 | 2 |
| B | 2 | 4 | H | 2 | 1.5 |
| C | 2 | 3.5 | I | 0 | — |
| D | 0 | J | 2 | 6 | |
| E | 1 | 2 | K | 2 | 2 |
| F | 5 | 2 | |||
参考答案:
第一次调整优化:在关键线路上取压缩单位时间增加费用最低的F工作为对象,压缩2d。
增加费用:(2×2)万元=4万元
第二次调整优化:工作A、C、H、J与B、F、I,同时成为关键工作,选择H工作和F工作为调整对象,各压缩2d。
增加费用:2×(1.5+2)万元=7万元
第三次调整优化:工作A、C、H、K,与B、F、J仍为关键工作,选择A工作和F工作作为调整对象,各压缩1d。
增加费用:1×(2+2)万元=4万元
优化后的关键线路为:
①→③→⑥→⑦→⑧(或关键工作为B、F、J)
和①→②→④→⑦→⑧(或关键工作为A、C、H、J)
工期:(98-2-2-1)d=93d
最低综合费用:(401+4+7+4)万元=416万元
