问题
填空题
已知平面向量
|
答案
∵
| a |
| b |
| c |
| 0 |
∴三个向量首尾相接后，构成一个三角形
且
| a |
| b |
| c |
| b |
| c |
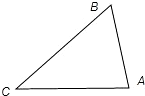
故所得三角形如下图示：
其中∠C=45°，∠A=60°，AB=2
∴|
| a |
| AB?Sin∠A |
| sin∠C |
| 6 |
故答案为：
| 6 |
搜题请搜索小程序“爱下问搜题”
已知平面向量
|
∵
| a |
| b |
| c |
| 0 |
∴三个向量首尾相接后，构成一个三角形
且
| a |
| b |
| c |
| b |
| c |
故所得三角形如下图示：
其中∠C=45°，∠A=60°，AB=2
∴|
| a |
| AB?Sin∠A |
| sin∠C |
| 6 |
故答案为：
| 6 |